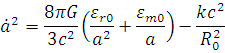
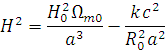
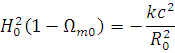
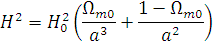
| Show that, for a universe without a cosmological constant, the scale factor a(t) will | |
| (i) reach a finite maximum value and then recollapse, if k > 0; | [1] |
| (ii) increase at an ever-decreasing rate, i.e. ȧ → 0 as t → ∞, if k = 0; | [1] |
| (iii) increase at a rate which tends to a constant value as t → ∞, if k < 0. | [1] |
| The Friedmann equation for the case where Λ = 0 is given by | |
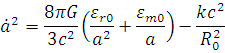 |
|
| For case (i), the first term is positive, tends to infinity as a → 0, and tends to zero as a → ∞. The second term is negative and of constant size. Therefore, at some finite value of a, the two terms must cancel out, giving ȧ = 0. Hence a reaches a finite maximum value, after which it must collapse under gravity. | [1] |
| For case (ii), the first term is positive, tends to infinity as a → 0, and tends to zero as a → ∞. The second term is zero. Therefore ȧ decreases from an initially very large value and tends to zero as a (or t) → ∞; i.e., the expansion rate decreases steadily with time, as required. | [1] |
| For case (iii), the first term is positive, tends to infinity as a → 0, and tends to zero as a → ∞. The second term is positive and constant. Therefore, as a → ∞, the expansion rate will tend to a constant value, because the first term will become negligible. | [1] |
| Define the density parameter Ω, and show that the three cases above correspond to Ω > 1, Ω = 1 and Ω < 1 respectively. | [3] |
| Ω = ε/εcrit where εcrit = 3c2H2/8πG. | [1] |
| Therefore the Friedmann equation can be written as H2 = H2Ωtot – kc2/R02, i.e. H2(1 – Ωtot) = –kc2/R02 | [1] |
| All the terms are squared, and therefore positive, except for (1 – Ωtot) on the LHS and -k on the RHS. Therefore, (i) if k > 0 we must have (1 – Ωtot) < 0, i.e. Ωtot > 1; (ii) if k = 0 we must have (1 – Ωtot) = 0, i.e. Ωtot = 1; (iii) if k < 0 we must have (1 – Ωtot) > 0, i.e. Ωtot < 1. | [1] |
| In case (i), calculate the maximum value of a if Ωr0 ≈ 0 and Ωm0 = 1.1. | [3] |
| We note that a = amax corresponds to ȧ = 0. | [0.5] |
| We now write H2Ωm = H02Ωm0/a3. Our Friedmann equation becomes | |
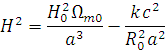 |
[0.5] |
| Applying this to the present time gives | |
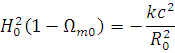 |
[0.5] |
| Substituting this back into the previous equation gives | |
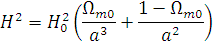 |
[0.5] |
| which we equate to zero and then solve to find amax = &Omegam0/(&Omegam0 – 1). Putting in the numbers gives amax = 11. | [1] |
(2006 Resit Q5(a).)